The excerpt note is about panoramic images from Zhang et al., 2007.

Zhang, A. M. (2007). Robust appearance based visual route following in large scale outdoor environments. Proceedings of the Australasian Conference on Robotics and Automation, Brisbane, Australia, 2007.

Image Pre-processing

Identical image pre-processing steps are applied to both reference and measurement images. Input colour image is first converted into greyscale (colour information is unstable under changing lighting conditions) then “un-warped” (i.e. remapped) onto azimuth-elevation coordinates. An example of the original colour image and its unwarped greyscale image is shown in Figures 3a and 3b respectively, where horizontal axis is azimuth and vertical axis is elevation. Vertical field of view is restricted to [-50 deg, 20 deg].

Fig. 3: (a) Original colour image. (b) Converted to greyscale and mapped into azimuth-elevation coordinates, where the azimuth-axis is horizontal. (c) Patch normalised to remove lighting variations, using a neighbourhood of 17 by 17 pixels.

Patch normalisation is then applied to compensate for changes in lighting condition. It transforms the pixel values as follows:

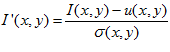(1)

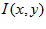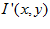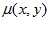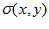Where and are the original and normalised pixels respectively, and are the mean and standard deviation of pixel values in a neighbourhood centred around 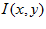. Figure 3c shows the result of applying patch normalisation to Figure 3b. A neighbourhood size of 17 by 17 pixels has worked well in the experiments.

Image Cross Correlation

The section addresses the problem of measuring an orientation difference between a measurement image and a reference image.

Orientation difference between reference and measurement image is therefore only a shift along the azimuth axis. This shift is recovered using Image Cross Correlation (ICC) performed efficiently in the Fourier domain. Let 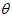denote azimuth and 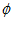elevation. The frontal 180 degree field view of the reference image serves as the template, i.e. 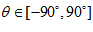. Let the search range be 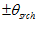such that the measurement image is limited to the angular range 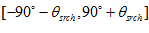. Because only a 1D cross-correlation along the azimuth axis is performed, each row in the image is transformed into Fourier domain separately. Reference image is padded with zeros to the same size as the measurement image. If the measurement image is 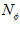by 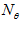pixels, then the Fourier domain image consists of 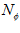sets of 1D Fourier coefficients, each of a single row. Algorithmic complexity for a single image is 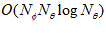. Convolution in spatial domain is equivalent to multiplication in Fourier domain:

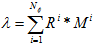
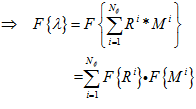
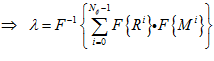(2)

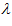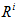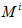Where is the Image Cross Correlation (ICC) coefficients, and are the i th row in the reference and measurement image respectively, * is the convolution operator and 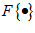is the Fourier transform operator. Equation 2 states that each corresponding row of the measurement and reference images are multiplied in Fourier domain. The results are then summed followed by an inverse Fourier transform to obtain the spatial domain cross-correlation coefficients. Complexity for the multiplication in Fourier domain is 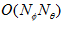and for inverse Fourier transform is 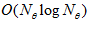. Fourier transforms for the reference images are calculated offline after the teaching run and stored. The complexity of a complete ICC is thus 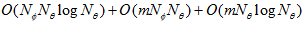where m is the number reference images to compare against. This is significantly better than the complexity of ICC performed in spatial domain which is 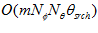. Comparing against 11 reference images only takes 2.3 ms on a 2.4GHz mobile Pentium 4 per measurement image.

For further more info, please read the Zhang 2007.

Zhang, A. M. (2007). Robust appearance based visual route following in large scale outdoor environments. Proceedings of the Australasian Conference on Robotics and Automation, Brisbane, Australia, 2007.