This is a brief excerpt note for studying the continuous attractor neural network (CANN) and 1D CANN for Head Direction.

The content is from the Wu, S., et al. review paper. (Wu, S., Wong, K.M., Fung, C.A., Mi, Y. and Zhang, W., 2016. Continuous attractor neural networks: candidate of a canonical model for neural information representation. F1000Research, 5.)

Summary

• A type of recurrent network, known as the continuous attractor neural network (CANN) or dynamic neural field, has received broad attention from computational neuroscientists.
• This model has been successfully applied to describe the encoding of continuous stimuli in neural systems, such as orientation (Ben-Yishai R. et al., 1995), moving direction (Georgopoulos A.P. et al., 1993), head direction (Zhang K. et al., 1996), and spatial location of objects (Samsonovich A. et al., 1997).
• The model has many computationally appealing properties, such as efficient population decoding (Deneve S. et al., 1999), smooth tracking of moving objects (Wu S. et al., 2005), and implementing parametrical working memory (Compter A. et al., 2000, and Wang XJ et al., 2001).

The model of CANNs

The CANN is a network model for neural information representation in which stimulus information is encoded in firing patterns of neurons, corresponding to stationary states (attractors) of the network.

Compared with other attractor models, such as the Hopfield network, the most prominent character of a CANN is its translation-invariant connections between neurons; that is, the connection strength between two neurons depends only on the difference between their preferred stimuli, rather than on the preferred stimulus values.

The translation-invariant connection structure enables a CANN to hold a continuous family of attractors (stationary states), rather than isolated ones, with each of the attractor states encoding a stimulus value. These states are often called bumps because of the localization of their activities in feature space. They form a submanifold of neutrally stable states in the state space of the network dynamics. This neutral stability endows a CANN with the capacity of updating its states (internal representations of stimuli) smoothly under the drive of an external input.

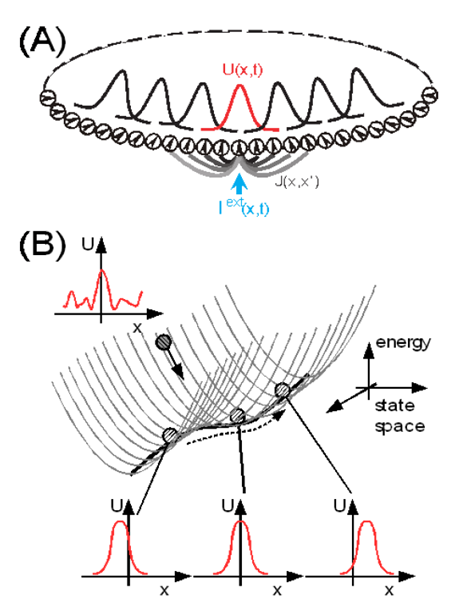
Figure 1. A continuous attractor neural network (CANN) model. (A) An illustration of a one dimensional CANN, which encodes a continuous variable (e.g. orientation or direction) x in the region of (-π,π] with the periodic condition. Neurons are aligned in the network according to their preferred stimuli. The neuronal connection pattern J(x,x’) is translation-invariant in the space. The network can hold a continuous family of bump-shaped stationary states. (B) The stationary states of the CANN form a subspace in which the network states are neutrally stable. The subspace is illustrated as a canyon in the state space of the network. The movement of the network state along the canyon corresponds to the position shift of a bump.

One Dimensional CANN for Head Direction

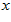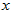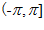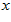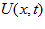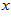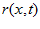Consider a one-dimensional continuous stimulus , such as head=direction or orientation ,encoded by an ensemble of neurons, and the value of is in the range of with a periodic boundary. In the space of stimulus , neurons are aligned in the network according to their preferred stimulus values. Denote as the synaptic input at time t of the neurons whose preferred stimulus is , and the neuronal firing rate. The dynamics of 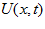are determined by the recurrent input from other neurons, its own relaxation, and an external input 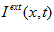, which is written as,

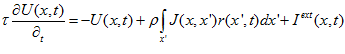(1)

Where 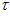is the synaptic time constant and 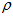the neuron density. 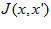is the interaction strength from neurons at 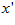to neurons at 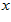, and is chosen to be 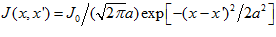, where the parameter 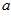controls the neuronal interaction range. Note that 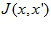is a function of 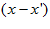;that is, the neuronal interaction is translation-invariant in the space of neuronal preferred stimuli. The neuronal firing rate 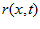is determined by the synaptic input according to

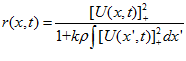(2)

Where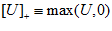 . The neuronal firing rate first increases with the input and then saturates gradually because of divisive normalization by the total network activity. In the absence of external input and for 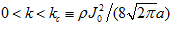, the network holds a continuous family of stationary states, which are written as 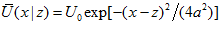and 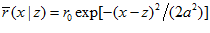. These stationary states are translationally invariant and have a Gaussian-bump shape with a free parameter 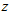indicating their positions.

The dynamical behaviors of a CANN can be readily analysed by a projection method by using the property that the dynamics of a CANN are dominated by a few motion modes, which correspond to distortions of the bump shape in terms of height, position, width, skewness, and so on in the bump shape (Figure 2). We can project the dynamics of a CANN onto these dominating modes and simplify the network dynamics significantly. Typically, by including one or two leading motion modes, the simplified dynamics are adequate to capture the main features of a CANN.

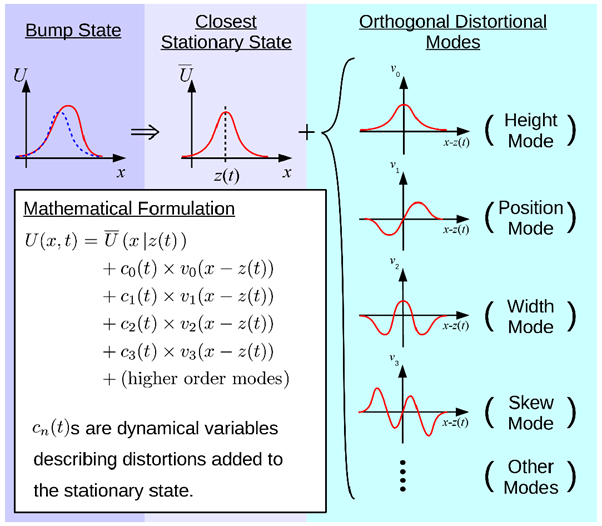
Figure 2. The projection method. The dynamics of a continuous attractor neural network are dominated by a few motion modes, corresponding to distortions of the bump shape in height, position, width, skewness, and so on. We can project the network dynamics on these dominating modes to simplify it significantly.

Relevant References

Ben-Yishai R, Bar-Or RL, Sompolinsky H: Theory of orientation tuning in visual cortex. Proc Natl Acad Sci U S A. 1995; 92(9): 3844–3848.

Georgopoulos AP, Taira M, Lukashin A: Cognitive neurophysiology of the motor cortex. Science. 1993; 260(5104): 47–52.

Zhang K: Representation of spatial orientation by the intrinsic dynamics of the head-direction cell ensemble: a theory. J Neurosci. 1996; 16(6): 2112–2126.

Samsonovich A, McNaughton BL: Path integration and cognitive mapping in a continuous attractor neural network model. J Neurosci. 1997; 17(15): 5900–5920.

Deneve S, Latham PE, Pouget A: Reading population codes: a neural implementation of ideal observers. Nat Neurosci. 1999; 2(8): 740–745.

Wu S, Amari S: Computing with continuous attractors: stability and online aspects. Neural Comput. 2005; 17(10): 2215–2239.

Compte A, Brunel N, Goldman-Rakic PS, et al.: Synaptic mechanisms and network dynamics underlying spatial working memory in a cortical network model. Cereb Cortex. 2000; 10(9): 910–923.

Wang XJ: Synaptic reverberation underlying mnemonic persistent activity. Trends Neurosci. 2001; 24(8) : 455–463.

Fung CC, Wong KY, Wu S: A moving bump in a continuous manifold: a comprehensive study of the tracking dynamics of continuous attractor neural networks. Neural Comput. 2010; 22(3): 752–792.

Wu S, Hamaguchi K, Amari S: Dynamics and computation of continuous attractors. Neural Comput. 2008; 20(4): 994–1025.

Goodridge JP, Touretzky DS: Modeling attractor deformation in the rodent head-direction system. J Neurophysiol. 2000; 83(6): 3402–3410.

Wimmer K, Nykamp DQ, Constantinidis C, et al.: Bump attractor dynamics in prefrontal cortex explains behavioral precision in spatial working memory. Nat Neurosci. 2014; 17(3): 431–439.