【Excerpt Note】Neuronal Population Coding of Movement Direction
Georgopoulos, Apostolos P., Andrew B. Schwartz, and Ronald E. Kettner. “Neuronal population coding of movement direction.” Science (1986): 1416-1419.
The blog is a brief summary of the neuronal population coding model for movement direction.
Brief Summary
-
Although individual neurons in the arm area of the primate motor cortex are only broadly tuned to a particular direction in three-dimensional space, the animal can very precisely control the movement of its arm.
-
The direction of movement was found to be uniquely predicted by the action of a population of motor cortical neurons.
-
When individual cells were represented as vectors that make weighted contributions along the axis of their preferred direction (according to changes in their activity during the movement under consideration) the resulting vector sum of all cell vectors (population vector) was in a direction congruent with the direction of movement.
-
This population vector can be monitored during various tasks, and similar measures in other neuronal populations could be of heuristic value where there is a neural representation of variables with vectorial attributes.
The Neuronal Population Coding Model
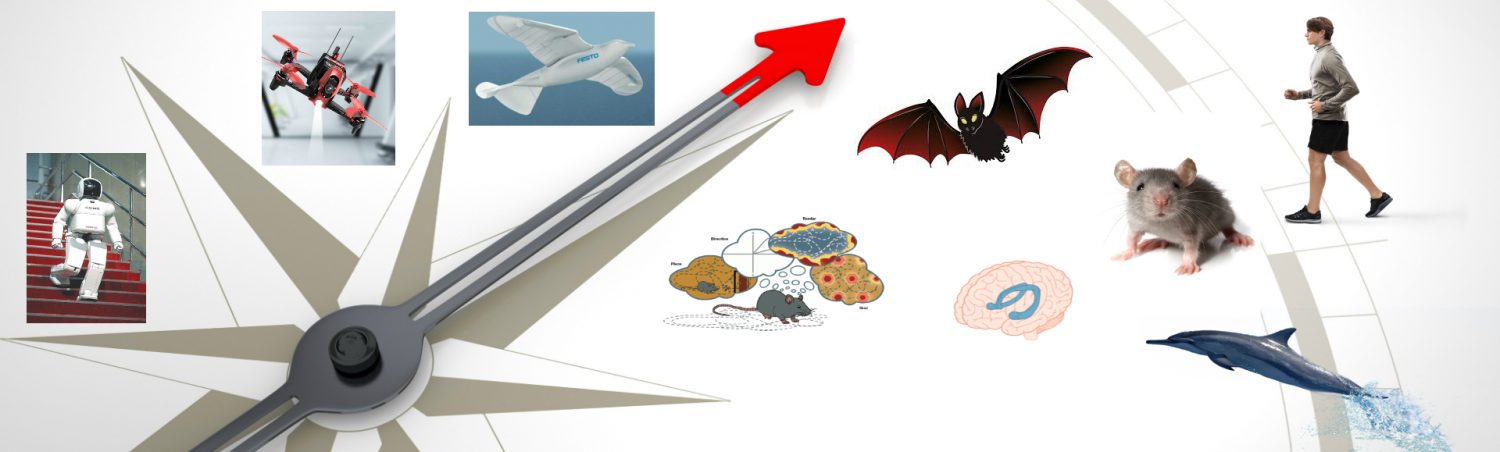
We used the following model to describe the relations between the activity of each directionally tuned neuron (Fig.1)and the direction of movement in 3D space. Let x, y, z be the positive axes of a Cartesian coordinate system with center at the origin of the movement. Consider a movement vector 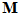 of unit length that makes angles
of unit length that makes angles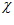 ,
, ,
, 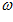 with the x, y, and z coordinate axes, respectively. The direction of vector
with the x, y, and z coordinate axes, respectively. The direction of vector 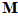 in 3-D space is specified by its direction cosines
in 3-D space is specified by its direction cosines 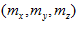 where
where 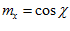 ,
, 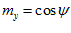 ,
,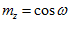 , and where
, and where 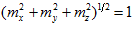 .
.
Fig. 1. Impulse activity of a single cell with movements in eight different directions indicated in the center drawing. Each line represents activity in one trial; eight trials for each movement direction are shown.
We used the following model to relate cell activity to movement direction.
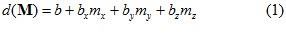
Where 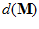 is the frequency of discharge of a particular neuron during movement in direction
is the frequency of discharge of a particular neuron during movement in direction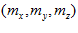 , and
, and 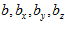 are coefficients that vary from neuron to neuron. The values of these coefficients and their standard errors were estimated with multiple regression techniques.
are coefficients that vary from neuron to neuron. The values of these coefficients and their standard errors were estimated with multiple regression techniques.
The model of Eq.1 implies that there is a particular movement vector 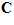 for which the cell’s activity will be highest. The direction of this vector is the cell’s preferred direction, which can be determined by estimating the direction cosines
for which the cell’s activity will be highest. The direction of this vector is the cell’s preferred direction, which can be determined by estimating the direction cosines 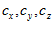 of the vector
of the vector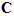 from Eq.1 as follws.
from Eq.1 as follws.
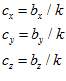
Where
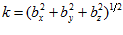
The preferred directions observed for the 224 neurons that fit the model ranged over the whole 3D directional continuum about the origin of the movement.
An equivalent expression of the model of Eq.1 is
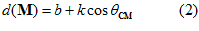
Where 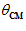 is the angle formed by the cell’s preferred direction
is the angle formed by the cell’s preferred direction and the direction of a particular movement
and the direction of a particular movement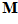 (Fig.2). It follows that the discharge rate,
(Fig.2). It follows that the discharge rate, 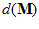 , will be highest with movements in the cell’s preferred direction, that is , when
, will be highest with movements in the cell’s preferred direction, that is , when 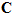 and
and 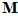 coincide (
coincide (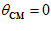 degrees,
degrees, 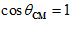 ); lowest with movements in the opposite direction (
); lowest with movements in the opposite direction (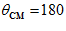 degrees,
degrees, 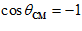 ); and in between with movements in intermediate directions (
); and in between with movements in intermediate directions (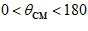 degrees,
degrees, 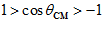 ). Equation 2 indicates that motor cortical cells are broadly tuned in the sense that they change their activity with movements in any direction.
). Equation 2 indicates that motor cortical cells are broadly tuned in the sense that they change their activity with movements in any direction.
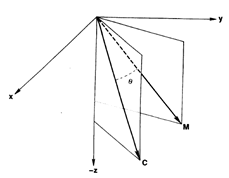
Fig.2. Schematic diagram to show the preferred direction () of the cell illustrated in Fig.1.
The direction of movement may be coded in a unique fashion by the neuronal ensemble. Consider a movement in an arbitrary direction . We want to find a way by which the neuronal population of the 224 directionally tuned cells with yield information about the direction of the movement
. We want to find a way by which the neuronal population of the 224 directionally tuned cells with yield information about the direction of the movement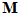 . For that purpose we made three assumptions. (i) Each cell (indexed by i) makes a vectorial contribution along its preferred direction,
. For that purpose we made three assumptions. (i) Each cell (indexed by i) makes a vectorial contribution along its preferred direction, 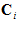 . (II) The magnitude of the contribution (or length of the vector)
. (II) The magnitude of the contribution (or length of the vector) 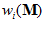 of the
of the 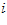 th cell is a function of the movement direction and is taken to be equal to the change in cell activity from an offset level.
th cell is a function of the movement direction and is taken to be equal to the change in cell activity from an offset level.
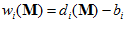
Where, from Eq.2, 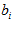 is a constant and
is a constant and 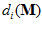 is the frequency of discharge of the ith cell for movement in direction
is the frequency of discharge of the ith cell for movement in direction 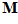 . From assumptions (i) and (ii), it follows that the weighted vectorial contribution of the ith cell is
. From assumptions (i) and (ii), it follows that the weighted vectorial contribution of the ith cell is
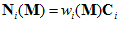
The vector 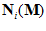 will point toward the ith cell’s preferred direction if the weight
will point toward the ith cell’s preferred direction if the weight 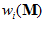 is positive or in the opposite direction if the weight is negative. (iii) Finally, we sum vectorially these cell vectors to obtain the neuronal population vector
is positive or in the opposite direction if the weight is negative. (iii) Finally, we sum vectorially these cell vectors to obtain the neuronal population vector 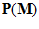 corresponding to movement direction
corresponding to movement direction 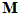 .
.
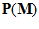 =
=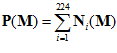
The outcome for one of the movement directions tested is shown in Fig. 3. The yellow line indicates the movement direction 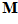 . The cluster of light purple lines represents 224 cell vectors (that is, the vectors
. The cluster of light purple lines represents 224 cell vectors (that is, the vectors 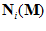 ,
, 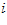 = 1 to 224) for movement direction
= 1 to 224) for movement direction 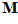 . The direction of the population vector
. The direction of the population vector 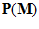 yielded by the vectorial summation of these cell vectors is orange. The direction of the population vector is very close to the direction of the movement vector(Fig.4). Therefore, the population vector predicts accurately the direction of the movement.
yielded by the vectorial summation of these cell vectors is orange. The direction of the population vector is very close to the direction of the movement vector(Fig.4). Therefore, the population vector predicts accurately the direction of the movement.

Fig3. Cluster of 224 single cell vectorial contributions (light purple lines) for one movement direction (yellow). The population vector is orange.
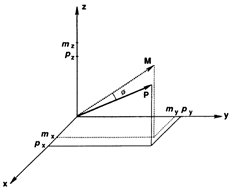
Fig. 4 Schematic diagram to show the directions of the population (P) and movement (M) vectors for the data in Fig.3. For illustration purposes, the population vector has been normalized so that both P and M are of unit length. Therefore, the direction cosines of these vectors equal their projections onto coordinate axes x, y, and z. These projections are shown as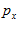 ,
, 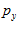 ,
,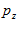 and
and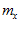 ,
,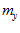 ,
,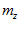 , for P and M, respectively. Also shown is the angle
, for P and M, respectively. Also shown is the angle 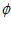 formed between the two vectors.
formed between the two vectors.
Conclusion
The population vector computed for the motor cortex during the waiting period is in a direction congruent with that of the upcoming movement.
The population vector can serve to monitor brain events during the spatial planning of the movement in space, in the absence of overt movement.
Single cells were broadly tuned to the direction of the stimulus in the visual field but the population vector predicted accurately the direction of the stimulus.
This result suggests that the population coding of motion direction proposed in the study may be of general significance to the problem of how directional information might be uniquely coded by neuronal ensembles.
About
Brain Inspired Navigation Blog
New discovery worth spreading on brain-inspired navigation in neurorobotics and neuroscience
Recent Posts
- How human, animals, robots encode and recall place?
- How the brain constructs time and space and how these are related to episodic memory?
- How environmental novelty modulate rapid cortical plasticity during navigation?
- How the Hippocampal Cognitive Map Supports Flexible Navigation?
- How the geometric structure and underlying circuit organization of hippocampal population dynamics facilitate both memory discrimination and generalization, enabling efficient and flexible learning?
Tags
Categories
- 3D Movement
- 3D Navigation
- 3D Path Integration
- 3D Perception
- 3D SLAM
- 3D Spatial Representation
- AI Navigation
- Bio-Inspired Robotics
- Brain Inspired Localization
- Brain-Inspired Navigation
- Cognitive Map
- Cognitive Navigation
- Episodic Memory
- Excerpt Notes
- Flying Vehicle Navigation
- Goal Representation
- Insect Navigation
- Learning to Navigate
- Memory
- Neural Basis of Navigation
- Path Integration
- Path Planning
- Project
- Research Tips
- Robotic Vision
- Self-Flying Vehicles
- Semantic Memory
- Spatial Cognition
- Spatial Cognitive Computing
- Spatial Coordinate System
- Spatial Learning
- Spatial Memory
- Spatial Resoning
- Time
- Unclassified
- Visual Cortex
- Visual Cue Cells
Links
- Laboratory of Nachum Ulanovsky
- Jeffery Lab
- BatLab
- The NeuroBat Lab
- Taube Lab
- Laurens Group
- Romani Lab
- Moser Group
- O’Keefe Group
- DoellerLab
- MilfordRobotics Group
- The Space and Memory group
- Angelaki Lab
- Spatial Cognition Lab
- McNaughton Lab
- Conradt Group
- The Fiete Lab
- The Cacucci Lab
- The Burak Lab
- Knierim Lab
- Clark Spatial Navigation & Memory Lab
- Computational Memory Lab
- The Dombeck Lab
- Zugaro Lab
- Insect Robotics Group
- The Nagel Lab
- Basu Lab
- Spatial Perception and Memory lab
- The Neuroecology lab
- The Nagel Lab
- Neural Modeling and Interface Lab
- Memory and Navigation Circuits Group
- Neural Circuits and Memory Lab
- The lab of Arseny Finkelstein
- The Epstein Lab
- The Theoretical Neuroscience Lab
- Gu Lab (Spatial Navigation and Memory)
- Fisher Lab (Neural Circuits for Navigation)
- The Alexander Lab (Spatial Cognition and Memory)
- Harvey Lab (Neural Circuits for Navigation)
- Buzsáki Lab
- Brain Computation & Behavior Lab
- ……